- Home
- About Ranking
- About Ranking (Methodology)
SchoolDigger.com Ranking Methodology
Summary:
SchoolDigger ranks schools by each school's Average Standard Score. The school with the highest Average Standard Score is ranked #1 in the state.
Why Standard Scores?
Comparing test scores from different grades and tests is problematic. As an example: from the table below, can you tell which school is performing best in math?
| School |
Grade |
Math % Proficient |
| Lincoln Elementary |
5th |
90.3 |
| Smith Elementary |
4th |
81.5 |
| Jefferson Elementary |
6th |
75.0 |
The truth is, we can't tell from this data. The 4th grade test may be much more difficult than the 5th grade test, and therefore a lower score might actually be the "better" one.
So for a better method in comparing proficiency scores across different grades and tests, we map these raw scores onto a
Standard Normal Distribution.
This statistical method maps these numbers onto the same shaped bell-curve so that
we
can compare scores from different grades and tests.
For a terrific explanation of the process and why it is useful, see
Standard Normal Distribution at mathisfun.com.
How we calculate a school's Average Standard Score.
We will now walk through the mathematical steps to calculate a school's Average Standard Score.
Let's use data from a fictional school: Smith Elementary in Topeka, Kansas.
In 4th grade math, Smith Elementary's students performed at an 81.5 percent proficiency level.
| Test |
Grade |
% Proficient |
| Math |
4th |
81.5% |
We first calculate a
Z-Score for Smith Elementary's 4th grade math score. A Z-Score is the multiple of standard deviations that Smith's 4th grade math score is from the 4th Kansas state mean (average) score. A positive Z-Score means
the school score is above the Kansas state mean score, and a negative Z-Score means the score is below the Kansas state mean score.
The Z-Score calculation is:
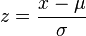
Where χ is the 4th grade math proficiency score, μ is the mean score of all Kansas 4th grade math scores, and σ is the standard deviation of the Kansas 4th grade math scores.
In our case, the mean score for Kansas 4th grade math statewide (μ) is 59.960, and the standard deviation (σ) is 18.018.
So, the calculated Z-Score for Smith Elementary is 1.195:
| Test |
Grade |
% Proficient |
State Mean Score |
State Standard
Deviation |
Z-Score |
| Math |
4th |
81.5% |
59.96 |
18.02 |
1.195 |
This Z-Score is then mapped using the
standard normal distribution, which gives us our Standard Score:
| Test |
Grade |
% Proficient |
State Mean Score |
State Standard
Deviation |
Z-Score |
Standard Score |
| Math |
4th |
81.5% |
59.96 |
18.02 |
1.195 |
87.12% |
We do this for all the tests from Smith Elementary and calculate an Average Standard Score:
| Test |
Grade |
% proficient |
State Average |
State Standard
Deviation |
Z-Score |
Standard Score |
| Math |
3rd |
85.90 |
64.38 |
17.09 |
1.26 |
89.60 |
| Math |
4th |
81.50 |
61.06 |
18.06 |
1.13 |
87.12 |
| Math |
5th |
68.90 |
61.83 |
17.08 |
0.41 |
66.07 |
| Math |
6th |
73.20 |
59.85 |
17.28 |
0.77 |
78.00 |
| Reading |
3rd |
87.20 |
72.78 |
14.47 |
1.00 |
84.05 |
| Reading |
4th |
87.30 |
71.78 |
14.45 |
1.07 |
85.86 |
| Reading |
5th |
83.60 |
72.14 |
14.70 |
0.78 |
78.23 |
| Reading |
6th |
77.50 |
71.15 |
14.21 |
0.45 |
67.26 |
| Science |
5th |
78.70 |
65.72 |
18.04 |
0.72 |
76.42 |
| Writing |
4th |
77.80 |
60.85 |
17.65 |
0.96 |
83.16 |
|
Average: |
79.58 |
So the final Average Standard Score for Smith Elementary is
79.58%. Our final ranking is based on this score, which is used in the rankings list:
| Rank |
School |
Average Standard Score |
| 1 |
Lincoln Elementary |
82.83 |
| 2 |
Smith Elementary |
79.58 |
| 3 |
Jefferson Elementary |
62.14 |
Helpful links

